3.交代形式：外積代数

ベクトルの積として、ウェッジ積を導入する。

と言いたいところだが、ウェッジ積の前に準備として置換について確認する必要がある。

$\sigma(i)$は置換と呼ばれ、ある集合の各元から別の（たまたま同じものになる場合もあるが）元に写す写像を表す。$\sigma$：$i \in I \to i’ \in I$

ここでは具体的には、$1$～$\lambda$の自然数１個ずつの集合$I$について適用している。この集合の元について、例えば$1$は$\sigma(1) = 5$に、$2$は$\sigma(2) = 3$に、$3$は$\sigma(3) = 3$に・・・という風に$\lambda$個の数１個１個を入れ換えるという意味である。$1 \leqq i \leqq \lambda$として、$i \in I$が移されて新たに割り当てられた数を$\sigma(i)$（$1 \leqq \sigma(i) \leqq \lambda$）と表記している。そして$\lambda$個の数は漏れなくダブリなく１対１対応で移されるので、重複を許さない$\lambda$個の順列$\lambda!$（$={}_\lambda \mathrm{P}_\lambda$）種類のパターンが存在する。（「置換」は英語では場合と数の「順列」と同じ”Permutation”である。なぜシグマを用いるのかはわからないが・・・。）$\lambda!$種類全ての置換のパターンの集合を$S_\lambda$とする。

例えば$I = \{1,2,3\}$ならば$S_\lambda = \{1,2,3\},\{2,3,1\},\{3,1,2\},\{1,3,2\},\{2,1,3\},\{3,2,1\}$の$3!=6$通りある。

また、置換には偶置換と奇置換があり、最初の並び$I=\{1,\cdots,\lambda\}$のいずれか２つを選んで入れ替える動作を繰り返して偶数回で実現される並びを偶置換、奇数回で実現される並びを奇置換という。必ず偶置換は偶置換、奇置換は奇置換であり、途中の入れ替え方が違っても 偶置換は必ず偶数回で、奇置換は必ず奇数回で実現される。“遠回り”して４回が６回に、５回が７回に、という ことはあるが、やはり偶置換は偶置換、奇置換は奇置換であることに変わりはない。置換で出来たある並びが２個の置換が何回で実現されたものか具体的に考えることは少ないが、通常は最低回数で表すことが通常だろう。なお、元の並びは０回置換で実現されている、つまり偶置換である。

因みに、$n \geqq 2$のとき$n$個の置換$n!$通りは偶数になるが、このうち半分が偶置換、半分が奇置換である。

$n$次元ベクトル$k$本のウェッジ積を以下のように定義する。

$\boldsymbol{p}_1,\cdots,\boldsymbol{p}_\lambda \in \mathbb{R}^n$とする。

$I = \{1,\cdots,\lambda\}$に対する置換$\sigma$の符号$\mathrm{sgn} (\sigma)$を、偶置換なら$+1$、奇置換なら$-1$とする。

$\boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_\lambda = \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn}(\sigma) \boldsymbol{p}_{\sigma(1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma(\lambda)}$

ぱっと見はどういう式なのか非常に分かりにくいだろう。私も慣れるまで時間がかかった。

後ろの部分は$\lambda$本のベクトルのテンソル積だが、添字が$i$ではなく$\sigma(i)$になっている。テンソル積は掛ける順序が異なれば
出来る式も異なって来るのだった。$\boldsymbol{p}_1$～$\boldsymbol{p}_\lambda$のテンソル積に違いないのだが、置換$\sigmaでi=1,2,\cdots,\lambda$の順序を入れ替えた$\sigma(i)=\sigma(1),\cdots,\sigma(\lambda)$の順番に従ってテンソル積を取るということである。

さらに$\mathrm{sgn} (\sigma)$が付いているので、偶置換ならそのままだが奇置換なら$-$符号が付く。

そして最後に$\displaystyle \sum_{\sigma \in S_\lambda}$で$\sigma$について全体の総和を取っている。$n!$通り全ての置換の組合せについてこの和を取るということである。

代数学のうちウェッジ積を扱うものを外積代数とかグラスマン代数と呼ぶ。

$0$次テンソルがただの実数であるのと同様、ただの実数と同じである。

$1$次テンソルがただのベクトルであるのと同様、ただのベクトルと同じである。

最初は$\boldsymbol{p}$と$\boldsymbol{q} \in \mathbb{R}^3$である場合、つまり$\boldsymbol{p} = p^1 \boldsymbol{e}_1 + p^2 \boldsymbol{e}_2 + p^3 \boldsymbol{e}_3,~\boldsymbol{q} = q^1 \boldsymbol{e}_1 + q^2 \boldsymbol{e}_2 + q^3 \boldsymbol{e}_3$である場合の$2$重ウェッジ積について具体的に考えてみよう。

$\mathbb{R}^3$の元の2重積からなる空間は$\wedge^2 \mathbb{R}^3$と表記する。

$\boldsymbol{p}$と$\boldsymbol{q}$のウェッジ積$\boldsymbol{p} \wedge \boldsymbol{q}$について、置換は$2!=2$通りで２個の総和になる。０回置換つまり偶置換の$\{1,2\}$については$\boldsymbol{p} \otimes \boldsymbol{q}$が、１回置換つまり奇置換の$\{2,1\}$については$-$を付して$- \boldsymbol{q} \otimes \boldsymbol{p}$が対応する。

よってこの場合の$2$重積は

$\boldsymbol{p} \wedge \boldsymbol{q} = \boldsymbol{p} \otimes \boldsymbol{q} – \boldsymbol{q} \otimes \boldsymbol{p}$

となり、テンソル積から順番を入れ替えたテンソル積を引いたものになった。

$2$項のテンソル積は$2$階テンソルである。テンソル積$\boldsymbol{p} \otimes \boldsymbol{q}$の$i,j$成分を$(\boldsymbol{p} \otimes \boldsymbol{q})^{ij}$のように表すと、$(\boldsymbol{p’} \otimes \boldsymbol{q’})^{ij} = {a^i}_k {a^j}_l (\boldsymbol{p} \otimes \boldsymbol{q})^{kl},~(\boldsymbol{q’} \otimes \boldsymbol{p’})^{ij} = {a^i}_k {a^j}_l (\boldsymbol{q} \otimes \boldsymbol{p})^{kl}$

となり、この差で表されるウェッジ積についても

$(\boldsymbol{p’} \otimes \boldsymbol{q’})^{ij} – (\boldsymbol{q’} \otimes \boldsymbol{p’})^{ij} = {a^i}_k {a^j}_l \{ (\boldsymbol{p} \otimes \boldsymbol{q})^{kl} – (\boldsymbol{q} \otimes \boldsymbol{p})^{kl} \}$

$(\boldsymbol{p’} \wedge \boldsymbol{q’})^{ij} = {a^i}_k {a^j}_l (\boldsymbol{p} \wedge \boldsymbol{q})^{kl}$

となるから、ウェッジ積（の$2$重積）は$2$階テンソルになる。

なお、ここでは反変ベクトル２本で作っているので$2$階反変テンソルである。

また、$2$階テンソルなので行列表示が可能である。

$\boldsymbol{p} \wedge \boldsymbol{q} =
\begin{pmatrix}
0 & p^1 q^2 – p^2 q^1 & p^1 q^3 – p^3 q^1\\
p^2 q^1 – p^1 q^2 & 0 & p^2 q^3 – p^3 q^2\\
p^3 q^1 – p^1 q^3 & p^3 q^2 – p^2 q^3 & 0
\end{pmatrix}$

２重ウェッジ積は２階テンソルなので、当然ながら双線型性をもつ。一応確認しておこう。

$(\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \wedge \boldsymbol{r} = \{ (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \otimes \boldsymbol{r} \} – \{ \boldsymbol{r} \otimes (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \}$

$= (\alpha \boldsymbol{p} \otimes \boldsymbol{r} + \beta \boldsymbol{q} \otimes \boldsymbol{r}) – (\alpha \boldsymbol{r} \otimes \boldsymbol{p} + \beta \boldsymbol{r} \otimes \boldsymbol{q})$

$= \alpha (\boldsymbol{p} \otimes \boldsymbol{r} – \boldsymbol{r} \otimes \boldsymbol{p}) + \beta (\boldsymbol{q} \otimes \boldsymbol{r} – \boldsymbol{r} \otimes \boldsymbol{q})$

$= \alpha \boldsymbol{p} \wedge \boldsymbol{r} – \beta \boldsymbol{q} \otimes \boldsymbol{r}$

よって$\boldsymbol{p}$と$\boldsymbol{q}$のウェッジ積は以下のように$3^2=9$項に書き下すことができる。

$\boldsymbol{p} \wedge \boldsymbol{q} = (p^1 \boldsymbol{e}_1 + p^2 \boldsymbol{e}_2 + p^3 \boldsymbol{e}_3) \wedge (q^1 \boldsymbol{e}_1 + q^2 \boldsymbol{e}_2 + q^3 \boldsymbol{e}_3)$

$= p^1 q^1 \boldsymbol{e}_1 \wedge \boldsymbol{e}_1 + p^1 q^2 \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 + p^1 q^3 \boldsymbol{e}_1 \wedge \boldsymbol{e}_3$

$+ p^2 q^1 \boldsymbol{e}_2 \wedge \boldsymbol{e}_1 + p^2 q^2 \boldsymbol{e}_2 \wedge \boldsymbol{e}_2 + p^2 q^3 \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

$+ p^3 q^1 \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + p^3 q^2 \boldsymbol{e}_3 \wedge \boldsymbol{e}_2 + p^3 q^3 \boldsymbol{e}_3 \wedge \boldsymbol{e}_3$

順番を入れ替えたウェッジ積について考えてみる。

$\boldsymbol{q} \wedge \boldsymbol{p} = \boldsymbol{q} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{q}$
となるので上の式と見比べると$\boldsymbol{p} \wedge \boldsymbol{q} = – \boldsymbol{q} \wedge \boldsymbol{p}$はすぐに分かるだろう。

特に同じものどうしのウェッジ積の場合、$\boldsymbol{p} \wedge \boldsymbol{p} = 0$。

（※後で述べるがウェッジ積は２階テンソルなので実数のように$0$と書いてしまうのは適切ではないかもしれないが、成分が全て$0$のテンソルということである。）

このような「積の順序を入れ替えると符号が入れ替わる。したがって同じものどうしの積は$0$」という性質を交代性（反対称性）と呼ぶ。

$\mathbb{R}^3$に属する任意のベクトルについてウェッジ積を取れるのだから基底の積も取れるはずであり、上と同様に

$\boldsymbol{e}_i \wedge \boldsymbol{e}_j = – \boldsymbol{e}_j \wedge \boldsymbol{e}_i$
$i = j$とすることで、$\boldsymbol{e}_i \wedge \boldsymbol{e}_i = 0$となる。

この性質を利用すると、先ほど$3^2=9$項の和として書き下した$\boldsymbol{p} \wedge \boldsymbol{q}$は、以下のようにまとめられることになる。

$\boldsymbol{p} \wedge \boldsymbol{q} = p^1 q^1 \boldsymbol{e}_1 \wedge \boldsymbol{e}_1 + p^1 q^2 \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 + p^1 q^3 \boldsymbol{e}_1 \wedge \boldsymbol{e}_3$

$+ p^2 q^1 \boldsymbol{e}_2 \wedge \boldsymbol{e}_1 + p^2 q^2 \boldsymbol{e}_2 \wedge \boldsymbol{e}_2 + p^2 q^3 \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

$+ p^3 q^1 \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + p^3 q^2 \boldsymbol{e}_3 \wedge \boldsymbol{e}_2 + p^3 q^3 \boldsymbol{e}_3 \wedge \boldsymbol{e}_3$

$= p^2 q^3 \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + p^3 q^2 \boldsymbol{e}_3 \wedge \boldsymbol{e}_2$

$+ p^3 q^1 \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + p^1 q^3 \boldsymbol{e}_1 \wedge \boldsymbol{e}_3$

$+ p^1 q^2 \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 + p^2 q^1 \boldsymbol{e}_2 \wedge \boldsymbol{e}_1$

$= (p^2 q^3 – p^3 q^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + (p^3 q^1 – p^1 q^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + (p^1 q^2 – p^2 q^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

普通のテンソル積の$2$重積なら項数は$3^2=9$項となるところが、交代性を持つウェッジ積では積の順番が逆になっている項が符号を逆にすることで同じ項にまとめられ、また同じものどうしの積が$0$になってしまう。結局、基底３つから異なる2つを取る組合せに等しい${}_3 \mathrm{C}_2=3$項になってしまうのである。

また行列表示についても、交代性に着目した書き方をすると次のようになる。

$\boldsymbol{p} \wedge \boldsymbol{q} =
\begin{pmatrix}
0 & p^1 q^2 – p^2 q^1 & p^1 q^3 – p^3 q^1\\
p^2 q^1 – p^1 q^2 & 0 & p^2 q^3 – p^3 q^2\\
p^3 q^1 – p^1 q^3 & p^3 q^2 – p^2 q^3 & 0
\end{pmatrix}
= \begin{pmatrix}
0 & p^1 q^2 – p^2 q^1 & -(p^3 q^1 – p^1 q^3)\\
-(p^1 q^2 – p^2 q^1) & 0 & p^2 q^3 – p^3 q^2\\
p^3 q^1 – p^1 q^3 & -(p^2 q^3 – p^3 q^2) & 0
\end{pmatrix}$

となる。この行列の$ij$成分の基底は$\boldsymbol{e}_i \otimes \boldsymbol{e}_j$である。この行列において、$ij$成分と$ji$成分で符号が逆の交代行列（反対称行列）になっており、対角成分は$0$である。

成分の変換則

${p’}^2 {q’}^3 – {p’}^3 {q’}^2 = ({a^2}_1 p^1 + {a^2}_2 p^2 + {a^2}_3 p^3)({a^3}_1 q^1 + {a^3}_2 q^2 + {a^3}_3 q^3) – ({a^3}_1 p^1 + {a^3}_2 p^2 + {a^3}_3 p^3)({a^2}_1 q^1 + {a^2}_2 q^2 + {a^2}_3 q^3)$

$= {a^2}_1 {a^3}_1 p^1 q^1 + {a^2}_1 {a^3}_2 p^1 q^2 + {a^2}_1 {a^2}_3 p^1 q^3$

$+ {a^2}_2 {a^3}_1 p^2 q^1 + {a^2}_2 {a^3}_2 p^2 q^2 + {a^2}_2 {a^2}_3 p^2 q^3$

$+ {a^2}_3 {a^3}_1 p^3 q^1 + {a^2}_3 {a^3}_2 p^3 q^2 + {a^2}_3 {a^2}_3 p^3 q^3$

$- {a^3}_1 {a^2}_1 p^1 q^1 – {a^3}_1 {a^2}_2 p^1 q^2 – {a^3}_1 {a^2}_3 p^1 q^3$

$- {a^3}_2 {a^2}_1 p^2 q^1 – {a^3}_2 {a^2}_2 p^2 q^2 – {a^3}_2 {a^2}_3 p^2 q^3$

$- {a^3}_3 {a^2}_1 p^3 q^1 – {a^3}_3 {a^2}_2 p^3 q^2 – {a^3}_3 {a^2}_3 p^3 q^3$

$= ({a^2}_2 {a^2}_3 – {a^3}_2 {a^2}_3)(p^2 q^3 – p^3 q^2)$

$+ ({a^2}_3 {a^3}_1 – {a^3}_3 {a^2}_1)(p^3 q^1 – p^1 q^3)$

$+ ({a^2}_1 {a^3}_2 – {a^3}_1 {a^2}_2)(p^1 q^2 – p^2 q^1)$

$= \tilde{a}_{11} (p^2 q^3 – p^3 q^2) + \tilde{a}_{12} (p^3 q^1 – p^1 q^3) + \tilde{a}_{13} (p^1 q^2 – p^2 q^1)$

同様に、

${p’}^3 {q’}^1 – {p’}^1 {q’}^3 = \tilde{a}_{21} (p^2 q^3 – p^3 q^2) + \tilde{a}_{22} (p^3 q^1 – p^1 q^3) + \tilde{a}_{23} (p^1 q^2 – p^2 q^1)$

${p’}^1 {q’}^2 – {p’}^2 {q’}^1 = \tilde{a}_{31} (p^2 q^3 – p^3 q^2) + \tilde{a}_{32} (p^3 q^1 – p^1 q^3) + \tilde{a}_{33} (p^1 q^2 – p^2 q^1)$

基底の変換則

$\boldsymbol{e’}_2 \wedge \boldsymbol{e’}_3 = ({b_2}^1 \boldsymbol{e}_1 + {b_2}^2 \boldsymbol{e}_2 + {b_2}^3 \boldsymbol{e}_3) \wedge ({b_3}^1 \boldsymbol{e}_1 + {b_3}^2 \boldsymbol{e}_2 + {b_3}^3 \boldsymbol{e}_3)$

$= {b_2}^1 {b_3}^1 \boldsymbol{e}_1 \wedge \boldsymbol{e}_1 + {b_2}^1  {b_3}^2 \boldsymbol{e}_1 \wedge \boldsymbol{e}_2+ {b_2}^1 {b_3}^3 \boldsymbol{e}_1 \wedge \boldsymbol{e}_3$

$+ {b_2}^2 {b_3}^1 \boldsymbol{e}_2 \wedge \boldsymbol{e}_1 + {b_2}^2 {b_3}^2 \boldsymbol{e}_2 \wedge \boldsymbol{e}_2 + {b_2}^2 {b_3}^3 \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

$+ {b_2}^3 {b_3}^1 \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + {b_2}^3 {b_3}^2 \boldsymbol{e}_3 \wedge \boldsymbol{e}_2 + {b_2}^3 {b_3}^3 \boldsymbol{e}_3 \wedge \boldsymbol{e}_3$

$= ({b_2}^2 {b_3}^3 – {b_2}^3 {b_3}^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

$+ ({b_2}^3 {b_3}^1 – {b_2}^1 {b_3}^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1$

$+ ({b_2}^1 {b_3}^2 – {b_2}^2 {b_3}^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$= \tilde{b}_{11} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{12} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{13} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

同様に、

$\boldsymbol{e’}_3 \wedge \boldsymbol{e’}_1 = \tilde{b}_{21} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{22} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{23} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$\boldsymbol{e’}_1 \wedge \boldsymbol{e’}_2 = \tilde{b}_{31} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{32} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{33} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

したがって、

$\boldsymbol{p’} \wedge \boldsymbol{q’} = ({p’}^2 {q’}^3 – {p’}^3 {q’}^2) \boldsymbol{e’}_2 \wedge \boldsymbol{e’}_3 + ({p’}^3 {q’}^1 – {p’}^1 {q’}^3) \boldsymbol{e’}_3 \wedge \boldsymbol{e’}_1 + ({p’}^1 {q’}^2 – {p’}^2 {q’}^1) \boldsymbol{e’}_1 \wedge \boldsymbol{e’}_2$

$= \{ \tilde{a}_{11} (p^2 q^3 – p^3 q^2) + \tilde{a}_{12} (p^3 q^1 – p^1 q^3) + \tilde{a}_{13} (p^1 q^2 – p^2 q^1) \} \{ \tilde{b}_{11} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{12} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{13} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 \}$

$+ \{ \tilde{a}_{21} (p^2 q^3 – p^3 q^2) + \tilde{a}_{22} (p^3 q^1 – p^1 q^3) + \tilde{a}_{23} (p^1 q^2 – p^2 q^1) \} \{ \tilde{b}_{21} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{22} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{23} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 \}$

$+ \{ \tilde{a}_{31} (p^2 q^3 – p^3 q^2) + \tilde{a}_{32} (p^3 q^1 – p^1 q^3) + \tilde{a}_{33} (p^1 q^2 – p^2 q^1) \} \{ \tilde{b}_{31} \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{b}_{32} \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{b}_{33} \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 \}$

$= \tilde{a}_{11} \tilde{b}_{11} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{11} \tilde{b}_{12} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{11} \tilde{b}_{13} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{12} \tilde{b}_{11} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{12} \tilde{b}_{12} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{12} \tilde{b}_{13} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{13} \tilde{b}_{11} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{13} \tilde{b}_{12} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{13} \tilde{b}_{13} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{21} \tilde{b}_{21} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{21} \tilde{b}_{22} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{21} \tilde{b}_{23} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{22} \tilde{b}_{21} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{22} \tilde{b}_{22} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{22} \tilde{b}_{23} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{23} \tilde{b}_{21} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{23} \tilde{b}_{22} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{23} \tilde{b}_{23} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{31} \tilde{b}_{31} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{31} \tilde{b}_{32} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{31} \tilde{b}_{33} (p^2 q^3 – p^3 q^2) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{32} \tilde{b}_{31} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{32} \tilde{b}_{32} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{32} \tilde{b}_{33} (p^3 q^1 – p^1 q^3) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$+ \tilde{a}_{33} \tilde{b}_{31} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + \tilde{a}_{33} \tilde{b}_{32} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + \tilde{a}_{33} \tilde{b}_{33} (p^1 q^2 – p^2 q^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$= (p^2 q^3 – p^3 q^2) \boldsymbol{e}_2 \wedge \boldsymbol{e}_3 + (p^3 q^1 – p^1 q^3) \boldsymbol{e}_3 \wedge \boldsymbol{e}_1 + (p^1 q^2 – p^2 q^1) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2$

$= \boldsymbol{p} \wedge \boldsymbol{q}$

よって、ウェッジ積$2$重積は$2$階テンソルの変換則に従う。すなわち、基底は変換行列2つによって変換され、成分はその逆行列の転置行列2つによって変換される。両者が逆の変換則に従うことで、成分と基底和として表したときはウェッジ積自体は変わらない。

ウェッジ積の導入部分において、ウェッジ積によって作られ交代性を有する$\boldsymbol{p} \wedge \boldsymbol{q} = (a^i \boldsymbol{e}_i) \wedge (b^j \boldsymbol{e}_j)$を考えたが、これは（$2$階）交代テンソル（あるいは反対称テンソル）である。より一般的に$p^{ij} \boldsymbol{e}_i \wedge \boldsymbol{e}_j$とすることもでき、これも交代テンソル（反対称テンソル）である。

交代性という条件を追加されたテンソルが座標変換を受けたとき交代性を保存することを、３次元における２階共変テンソルを例にとって確認してみた。

$2$階共変テンソル$p_{ij}$があり、交代性$p_{ij}=-p_{ji}$（したがって$p_{ii}=0$）が成り立っているとする。

$2$階共変テンソルなので変換行列$A=(a_{ij})$２個で${p’}_{kl} = {a_k}^i {a_l}^j p_{ij}$という形で変換される。交代性に注意して、具体的に${p’}_{kl}$の各成分を調べてみると

${p’}_{ii}$については、

${p’}_{11}$

$= {a_1}^1 {a_1}^1 p_{11} + {a_1}^1 {a_1}^2 p_{12} + {a_1}^1 {a_1}^3 p_{13}$

$+ {a_1}^2 {a_1}^1 p_{21} + {a_1}^2 {a_1}^2 p_{22} + {a_1}^2 {a_1}^3 p_{23}$

$+ {a_1}^3 {a_1}^1 p_{31} + {a_1}^3 {a_1}^2 p_{32} + {a_1}^3 {a_1}^3 p_{33}$

$= 0 + {a_1}^1 {a_1}^2 p_{12} – {a_1}^3 {a_1}^1 p_{31}$

$- {a_1}^1 {a_1}^2 p_{12} + 0 + {a_1}^2 {a_1}^3 p_{23}$

$+ {a_1}^3 {a_1}^1 p_{31} – {a_1}^2 {a_1}^3 p_{23} + 0$

$=0$

同様にして${p’}_{22}=0,{p’}_{33}=0$も示すことができる。

また、${p’}_{ij}~(i \neq j)$については、

${p’}_{12}$

$= {a_1}^1 {a_2}^1 p_{11} + {a_1}^1 {a_2}^2 p_{12} + {a_1}^1 {a_2}^3 p_{13}$

$+ {a_1}^2 {a_2}^1 p_{21} + {a_1}^2 {a_2}^2 p_{22} + {a_1}^2 {a_2}^3 p_{23}$

$+ {a_1}^3 {a_2}^1 p_{31} + {a_1}^3 {a_2}^2 p_{32} + {a_1}^3 {a_2}^3 p_{33}$

$= 0 + {a_1}^1 {a_2}^2 p_{12} – {a_1}^1 {a_2}^3 p_{31}$

$- {a_1}^2 {a_2}^1 p_{12} + 0 + {a_1}^2 {a_2}^3 p_{23}$

$+ {a_1}^3 {a_2}^1 p_{31} – {a_1}^3 {a_2}^2 p_{23} + 0$

$= ({a_1}^2 {a_2}^3 – {a_1}^3 {a_2}^2) p_{23} + ({a_1}^3 {a_2}^1 – {a_1}^1 {a_2}^3) p_{31} + ({a_1}^1 {a_2}^2 – {a_1}^2 {a_2}^1) p_{12}$

であり、一方、

${p’}_{21}$

$= {a_2}^1 {a_1}^1 p_{11} + {a_2}^1 {a_1}^2 p_{12} + {a_2}^1 {a_1}^3 p_{13}$

$+ {a_2}^2 {a_1}^1 p_{21} + {a_2}^2 {a_1}^2 p_{22} + {a_2}^2 {a_1}^3 p_{23}$

$+ {a_2}^3 {a_1}^1 p_{31} + {a_2}^3 {a_1}^2 p_{32} + {a_2}^3 {a_1}^3 p_{33}$

$= 0 + {a_2}^1 {a_1}^2 p_{12} – {a_2}^1 {a_1}^3 p_{31}$

$- {a_2}^2 {a_1}^1 p_{12} + 0 + {a_2}^2 {a_1}^3 p_{23}$

$+ {a_2}^3 {a_1}^1 p_{31} – {a_2}^3 {a_1}^2 p_{23} + 0$

$= ({a_2}^2 {a_1}^3 – {a_2}^3 {a_1}^2) p_{23} + ({a_2}^3 {a_1}^1 – {a_2}^1 {a_1}^3) p_{31} + ({a_2}^1 {a_1}^2 – {a_2}^2 {a_1}^1) p_{12}$

となるので、${p’}_{12}=-{p’}_{21}$

同様にして${p’}_{23}=-{p’}_{32},{p’}_{31}=-{p’}_{13}$も示すことができる。

よって、$p_{ij}$が交代性を持つとき、座標変換後の${p’}_{kl}$も交代性を持つことが確認できた。

ついでに、$p_{ij} x^i y^j$が縮約により添字がなくなってスカラーになり、座標変換しても値が変わらないことも確認してみる。

一方、変換則を考える。

共変成分が$A$で変換されるとすると、${p’}_{kl} = {a_k}^i {a_l}^j p_{ij}$

反変成分は${}^TA^{-1}={}^TB$で変換され、${x’}^k={b_i}^k x^i~{y’}^l={b_j}^l y^j$なので

${p’}_{kl} {x’}^k {y’}^l = ({a_k}^i {a_l}^j p_{ij})({b_i}^k x^i)({b_j}^l y^j)$

先ほどの考察で$P$の交代性が$P’$にも継承されることを確認したので、これを踏まえて

$= \{({b_1}^1 {b_2}^2 – {b_1}^2 {b_2}^1) x^1 y^2 + ({b_1}^1 {b_3}^2 – {b_1}^2 {b_3}^1) x^1 y^3 + ({b_2}^1 {b_1}^2 – {b_2}^2 {b_1}^1) x^2 y^1 + ({b_2}^1 {b_3}^2 – {b_2}^2 {b_3}^1) x^2 y^3 + ({b_3}^1 {b_1}^2 – {b_3}^2 {b_1}^1) x^3 y^1 + ({b_3}^1 {b_2}^2 – {b_3}^2 {b_2}^1) x^3 y^2\} \{({a_1}^1 {a_2}^2 – {a_1}^2 {a_2}^1) p_{12} + ({a_1}^2 {a_2}^3 – {a_1}^3 {a_2}^2) p_{23} + ({a_1}^3 {a_2}^1 – {a_1}^1 {a_2}^3) p_{31}\}$

$+ \{({b_1}^2 {b_2}^3 – {b_1}^3 {b_2}^2) x^1 y^2 + ({b_1}^2 {b_3}^3 – {b_1}^3 {b_3}^2) x^1 y^3 + ({b_2}^2 {b_1}^3 – {b_2}^3 {b_1}^2) x^2 y^1 + ({b_2}^2 {b_3}^3 – {b_2}^3 {b_3}^2) x^2 y^3 + ({b_3}^2 {b_1}^3 – {b_3}^3 {b_1}^2) x^3 y^1 + ({b_3}^2 {b_2}^3 – {b_3}^3 {b_2}^2) x^3 y^2\} \{({a_2}^1 {a_3}^2 – {a_2}^2 {a_3}^1) p_{12} + ({a_2}^2 {a_3}^3 – {a_2}^3 {a_3}^2) p_{23} + ({a_2}^3 {a_3}^1 – {a_2}^1 {a_3}^3) p_{31}\}$

$+ \{({b_1}^3 {b_2}^1 – {b_1}^1 {b_2}^3) x^1 y^2 + ({b_1}^3 {b_3}^1 – {b_1}^1 {b_3}^3) x^1 y^3 + ({b_2}^3 {b_1}^1 – {b_2}^1 {b_1}^3) x^2 y^1 + ({b_2}^3 {b_3}^1 – {b_2}^1 {b_3}^3) x^2 y^3 + ({b_3}^3 {b_1}^1 – {b_3}^1 {b_1}^3) x^3 y^1 + ({b_3}^3 {b_2}^1 – {b_3}^1 {b_2}^3) x^3 y^2\} \{({a_3}^1 {a_1}^2 – {a_3}^2 {a_1}^1) p_{12} + ({a_3}^2 {a_1}^3 – {a_3}^3 {a_1}^2) p_{23} + ({a_3}^3 {a_1}^1 – {a_3}^1 {a_1}^3) p_{31}\}$

$= (\tilde{b’}[33] x^1 y^2 + \tilde{b’}[23] x^1 y^3 – \tilde{b’}[33] x^2 y^1 + \tilde{b’}[13] x^2 y^3 – \tilde{b’}[23] x^3 y^1 – \tilde{b’}[13] x^3 y^2) ( \tilde{a’}[33] p_{12} + \tilde{a’}[31] p_{23} – \tilde{a’}[32] p_{31})$

$+ (\tilde{b’}[31] x^1 y^2 + \tilde{b’}[21] x^1 y^3 – \tilde{b’}[31] x^2 y^1 + \tilde{b’}[11] x^2 y^3 – \tilde{b’}[21] x^3 y^1 – \tilde{b’}[11] x^3 y^2)( \tilde{a’}[13] p_{12} + \tilde{a’}[11] p_{11} – \tilde{a’}[12] p_{31})$

$+ ( – \tilde{b’}[32] x^1 y^2 – \tilde{b’}[22] x^1 y^3 + \tilde{b’}[32] x^2 y^1 – \tilde{b’}[12] x^2 y^3 + \tilde{b’}[22] x^3 y^1 + \tilde{b’}[12] x^3 y^2)( – \tilde{a’}[23] p_{12} – \tilde{a’}[21] p_{11} + \tilde{a’}[22] p_{31})$

$= \{\tilde{b’}[33] \tilde{a’}[33] + \tilde{b’}[31] \tilde{a’}[13] + (-\tilde{b’}[32])(-\tilde{a’}[23])\} x^1 y^2 p_{12}$

$+ \{\tilde{b’}[23] \tilde{a’}[33] + \tilde{b’}[21] \tilde{a’}[13] + (-\tilde{b’}[22])(-\tilde{a’}[23])\} x^1 y^3 p_{12}$

$+ \{(-\tilde{b’}[33]) \tilde{a’}[33] + (-\tilde{b’}[31]) \tilde{a’}[13] + \tilde{b’}[32] (-\tilde{a’}[23])\} x^2 y^1 p_{12}$

$+ \{\tilde{b’}[13] \tilde{a’}[33] + \tilde{b’}[11] \tilde{a’}[13] + (-\tilde{b’}[12])(-\tilde{a’}[23])\} x^2 y^3 p_{12}$

$+ \{(-\tilde{b’}[23]) \tilde{a’}[33] + (-\tilde{b’}[21]) \tilde{a’}[13] + \tilde{b’}[22] (-\tilde{a’}[23])\} x^3 y^1 p_{12}$

$+ \{(-\tilde{b’}[13]) \tilde{a’}[33] + (-\tilde{b’}[11]) \tilde{a’}[13] + \tilde{b’}[12] (-\tilde{a’}[23])\} x^3 y^2 p_{12}$

$+ \{\tilde{b’}[33] \tilde{a’}[31] + \tilde{b’}[31] \tilde{a’}[11] + (-\tilde{b’}[32])(-\tilde{a’}[21])\} x^1 y^2 p_{23}$

$+ \{\tilde{b’}[23] \tilde{a’}[31] + \tilde{b’}[21] \tilde{a’}[11] + (-\tilde{b’}[22])(-\tilde{a’}[21])\} x^1 y^3 p_{23}$

$+ \{(-\tilde{b’}[33]) \tilde{a’}[31] + (-\tilde{b’}[31]) \tilde{a’}[11] + \tilde{b’}[32] (-\tilde{a’}[21])\} x^2 y^1 p_{23}$

$+ \{\tilde{b’}[13] \tilde{a’}[31] + \tilde{b’}[11] \tilde{a’}[11] + (-\tilde{b’}[12])(-\tilde{a’}[21])\} x^2 y^3 p_{23}$

$+ \{(-\tilde{b’}[23]) \tilde{a’}[31] + (-\tilde{b’}[21]) \tilde{a’}[11] + \tilde{b’}[22] (-\tilde{a’}[21])\} x^3 y^1 p_{23}$

$+ \{(-\tilde{b’}[13]) \tilde{a’}[31] + (-\tilde{b’}[11]) \tilde{a’}[11] + \tilde{b’}[12] (-\tilde{a’}[21])\} x^3 y^2 p_{23}$

$+ \{\tilde{b’}[33] (-\tilde{a’}[32]) + \tilde{b’}[31] (-\tilde{a’}[12]) + (-\tilde{b’}[32]) \tilde{a’}[22]\} x^1 y^2 p_{31}$

$+ \{\tilde{b’}[23] (-\tilde{a’}[32]) + \tilde{b’}[21] (-\tilde{a’}[12]) + (-\tilde{b’}[22]) \tilde{a’}[22]\} x^1 y^3 p_{31}$

$+ \{(-\tilde{b’}[33])(-\tilde{a’}[32]) + (-\tilde{b’}[31])(-\tilde{a’}[12]) + \tilde{b’}[32] \tilde{a’}[22]\} x^2 y^1 p_{31}$

$+ \{\tilde{b’}[13] (-\tilde{a’}[32]) + \tilde{b’}[11] (-\tilde{a’}[12]) + (-\tilde{b’}[12]) \tilde{a’}[22]\} x^2 y^3 p_{31}$

$+ \{(-\tilde{b’}[23])(-\tilde{a’}[32]) + (-\tilde{b’}[21])(-\tilde{a’}[12]) + \tilde{b’}[22] \tilde{a’}[22]\} x^3 y^1 p_{31}$

$+ \{(-\tilde{b’}[13])(-\tilde{a’}[32]) + (-\tilde{b’}[11])(-\tilde{a’}[12]) + \tilde{b’}[12] \tilde{a’}[22]\} x^3 y^2 p_{31}$

上記の行列の余因子の関係式を適用すると

$= x^1 y^2 p_{12} – x^2 y^1 p_{12} + x^2 y^3 p_{23} – x^3 y^2 p_{23} + x^3 y^1 p_{31} – x^1 y^3 p_{31}$

$= (x^1 y^2 – x^2 y^1) p_{12} + (x^2 y^3 + x^3 y^2) p_{23} + (x^3 y^1 – x^1 y^3) p_{31}$

$= p_{ij} x^i y^j$

続いて、$\mathbb{R}^3$の元の$3$重積について考える。$\mathbb{R}^3$の元の$3$重積からなる空間は$\wedge^3 \mathbb{R}^3$と表記する。

任意の3本のベクトル$\boldsymbol{p}=p^i \boldsymbol{e}_i,~\boldsymbol{q}=q^j \boldsymbol{e}_j,~\boldsymbol{r}=r^k \boldsymbol{e}_k$のウェッジ積について、置換は$3!=6$通り。

偶置換：$\{1,2,3\},\{2,3,1\},\{3,1,2\}$（元の並びと同じ向きの循環）

奇置換：$\{1,3,2\},\{2,1,3\},\{3,2,1\}$（元の並びと逆向きの循環）

よって以下のようになる。

$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r} = \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} + \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} + \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q} – \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} – \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r} – \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p}$

3項のテンソル積は$3$階テンソルである。テンソル積$\boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r}$の$i,j,k$成分を$(\boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r})^{ijk}$のように表すと、

$(\boldsymbol{p’} \otimes \boldsymbol{q’} \otimes \boldsymbol{r’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r})^{lmn}$

$(\boldsymbol{q’} \otimes \boldsymbol{r’} \otimes \boldsymbol{p’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p})^{lmn}$

$(\boldsymbol{r’} \otimes \boldsymbol{p’} \otimes \boldsymbol{q’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q})^{lmn}$

$(\boldsymbol{p’} \otimes \boldsymbol{r’} \otimes \boldsymbol{q’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q})^{lmn}$

$(\boldsymbol{q’} \otimes \boldsymbol{p’} \otimes \boldsymbol{r’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r})^{lmn}$

$(\boldsymbol{r’} \otimes \boldsymbol{q’} \otimes \boldsymbol{p’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p})^{lmn}$

となり、この和と差で表されるウェッジ積についても

$(\boldsymbol{p’} \otimes \boldsymbol{q’} \otimes \boldsymbol{r’})^{ijk} + (\boldsymbol{q’} \otimes \boldsymbol{r’} \otimes \boldsymbol{p’})^{ijk} + (\boldsymbol{r’} \otimes \boldsymbol{p’} \otimes \boldsymbol{q’})^{ijk} – (\boldsymbol{p’} \otimes \boldsymbol{r’} \otimes \boldsymbol{q’})^{ijk} – (\boldsymbol{q’} \otimes \boldsymbol{p’} \otimes \boldsymbol{r’})^{ijk} – (\boldsymbol{r’} \otimes \boldsymbol{q’} \otimes \boldsymbol{p’})^{ijk}$

$= {a^i}_l {a^j}_m {a^k}_n \{ (\boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r})^{lmn} + (\boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p})^{lmn} + (\boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q})^{lmn} – (\boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q})^{lmn} – (\boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r})^{lmn} – (\boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p})^{lmn} \}$

したがって

$(\boldsymbol{p’} \wedge \boldsymbol{q’} \wedge \boldsymbol{r’})^{ijk} = {a^i}_l {a^j}_m {a^k}_n (\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r})^{lmn}$

となるから、$3$重ウェッジ積は$3$階テンソルになる。

なお、ここでは反変ベクトル3本で作っているので$3$階反変テンソルである。

$3$重ウェッジ積は$3$階テンソルなので、当然ながら$3$重線型性を持つ。一応確認しておこう。

$(\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \wedge \boldsymbol{u} \wedge \boldsymbol{v}$

$= (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \otimes \boldsymbol{u} \otimes \boldsymbol{v} + \boldsymbol{u} \otimes \boldsymbol{v} \otimes (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) + \boldsymbol{v} \otimes (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \otimes \boldsymbol{u}$

$- (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \otimes \boldsymbol{v} \otimes \boldsymbol{u} – \boldsymbol{u} \otimes (\alpha \boldsymbol{p} + \beta \boldsymbol{q}) \otimes \boldsymbol{v} – \boldsymbol{v} \otimes \boldsymbol{u} \otimes (\alpha \boldsymbol{p} + \beta \boldsymbol{q})$

$= \alpha \boldsymbol{p} \otimes \boldsymbol{u} \otimes \boldsymbol{v} + \beta \boldsymbol{q} \otimes \boldsymbol{u} \otimes \boldsymbol{v}$

$+ \alpha \boldsymbol{u} \otimes \boldsymbol{v} \otimes \boldsymbol{p} + \beta \boldsymbol{u} \otimes \boldsymbol{v} \otimes \boldsymbol{q}$

$+ \alpha \boldsymbol{v} \otimes \boldsymbol{p} \otimes \boldsymbol{u} + \beta \boldsymbol{v} \otimes \boldsymbol{q} \otimes \boldsymbol{u}$

$- \alpha \boldsymbol{p} \otimes \boldsymbol{v} \otimes \boldsymbol{u} – \beta \boldsymbol{q} \otimes \boldsymbol{v} \otimes \boldsymbol{u}$

$- \alpha \boldsymbol{u} \otimes \boldsymbol{p} \otimes \boldsymbol{v} – \beta \boldsymbol{u} \otimes \boldsymbol{q} \otimes \boldsymbol{v}$

$- \alpha \boldsymbol{v} \otimes \boldsymbol{u} \otimes \boldsymbol{p} – \beta \boldsymbol{v} \otimes \boldsymbol{u} \otimes \boldsymbol{q}$

$= \alpha (\boldsymbol{p} \otimes \boldsymbol{u} \otimes \boldsymbol{v} + \boldsymbol{u} \otimes \boldsymbol{v} \otimes \boldsymbol{p} + \boldsymbol{v} \otimes \boldsymbol{p} \otimes \boldsymbol{u} – \boldsymbol{p} \otimes \boldsymbol{v} \otimes \boldsymbol{u} – \boldsymbol{u} \otimes \boldsymbol{p} \otimes \boldsymbol{v} – \boldsymbol{v} \otimes \boldsymbol{u} \otimes \boldsymbol{p})$

$+ \beta (\boldsymbol{q} \otimes \boldsymbol{u} \otimes \boldsymbol{v} + \boldsymbol{u} \otimes \boldsymbol{v} \otimes \boldsymbol{q} + \boldsymbol{v} \otimes \boldsymbol{q} \otimes \boldsymbol{u} – \boldsymbol{q} \otimes \boldsymbol{v} \otimes \boldsymbol{u} – \boldsymbol{u} \otimes \boldsymbol{q} \otimes \boldsymbol{v} – \boldsymbol{v} \otimes \boldsymbol{u} \otimes \boldsymbol{q})$

$= \alpha (\boldsymbol{p} \wedge \boldsymbol{u} \wedge \boldsymbol{v}) + \beta (\boldsymbol{q} \wedge \boldsymbol{u} \wedge \boldsymbol{v})$

テンソル$3$重積は$3$重線型性を持つので、その加法と減法で表されたウェッジ積の$3$重積も$3$重線型性を持つ。

このことを踏まえて一般のベクトルの$3$重ウェッジ積を計算してみると

$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r}$

$= \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} + \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} + \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q} – \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} – \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{q}$

$= (p^1 q^2 r^3 + p^2 q^3 r^1 + p^3 q^1 r^2 – p^3 q^2 r^1 – p^1 q^3 r^2 – p^2 q^1 r^3) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

$3^3 \times 6 = 162$項もあるので真面目に全部書き下して計算などできたものではない。だが$2$重積と同様に、テンソル積を経由せずに計算できる。$i=1$～$3,~j=1$～$3~k=1$～$3$で縮約を取って

$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r}$

$= \{(p^i \boldsymbol{e}_i) \wedge (q^j \boldsymbol{e}_j)\} \wedge (r^k \boldsymbol{e}_k)$

$= p^i q^j r^k \boldsymbol{e}_i \wedge \boldsymbol{e}_j \wedge \boldsymbol{e}_k$

$= (p^1 q^2 r^3 + p^2 q^3 r^1 + p^3 q^1 r^2 – p^3 q^2 r^1 – p^1 q^3 r^2 – p^2 q^1 r^3) \boldsymbol{e}_1 \wedge \boldsymbol{e}_2 \wedge \boldsymbol{e}_3$

項数はテンソル積の$3$重積なら$3^3=27$個となるところが、ウェッジ積の場合は3つの基底から3つを取る組合せなので${}_3 \mathrm{C}_3=1$個になってしまう。

順序を入れ替えて３重積を取ってみると、以下の通りとなる。

$\boldsymbol{q} \wedge \boldsymbol{r} \wedge \boldsymbol{p} = \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} + \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q} + \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} – \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r} – \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{p}$

$\boldsymbol{r} \wedge \boldsymbol{p} \wedge \boldsymbol{q} = \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q} + \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} + \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} – \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} – \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r}$

$\boldsymbol{p} \wedge \boldsymbol{r} \wedge \boldsymbol{q} = \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} + \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} + \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r} – \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} – \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} – \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q}$

$\boldsymbol{q} \wedge \boldsymbol{p} \wedge \boldsymbol{r} = \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r} + \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} + \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} – \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r} – \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q}$

$\boldsymbol{r} \wedge \boldsymbol{q} \wedge \boldsymbol{p} = \boldsymbol{r} \otimes \boldsymbol{q} \otimes \boldsymbol{p} + \boldsymbol{q} \otimes \boldsymbol{p} \otimes \boldsymbol{r} + \boldsymbol{p} \otimes \boldsymbol{r} \otimes \boldsymbol{q} – \boldsymbol{r} \otimes \boldsymbol{p} \otimes \boldsymbol{q} – \boldsymbol{q} \otimes \boldsymbol{r} \otimes \boldsymbol{p} – \boldsymbol{p} \otimes \boldsymbol{q} \otimes \boldsymbol{r}$

したがって

$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r} = \boldsymbol{q} \wedge \boldsymbol{r} \wedge \boldsymbol{p} = \boldsymbol{r} \wedge \boldsymbol{p} \wedge \boldsymbol{q} = – \boldsymbol{p} \wedge \boldsymbol{r} \wedge \boldsymbol{q} = – \boldsymbol{q} \wedge \boldsymbol{p} \wedge \boldsymbol{r} = – \boldsymbol{r} \wedge \boldsymbol{q} \wedge \boldsymbol{p}$

が成り立つが、これは$\boldsymbol{p}, \boldsymbol{q}, \boldsymbol{r}$を同じ循環で入れ替えても同じで、逆の循環にすると符号が反転することを示している。

ここで例えば

$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{r} = – \boldsymbol{p} \wedge \boldsymbol{r} \wedge \boldsymbol{q}$

について$\boldsymbol{r} = \boldsymbol{q}$とすると$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{q} = – \boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{q}$より$\boldsymbol{p} \wedge \boldsymbol{q} \wedge \boldsymbol{q} = 0$となる。同様の計算により、ベクトル3本のうち2本以上が同じものの場合は全て$0$になる。

このように、$\wedge^\lambda \mathbb{R}^3$の元の項数は$3$個の基底から$\lambda$個を取る組合せなので、${}_3 \mathrm{C}_\lambda$個になる。したがって、$\lambda=0,1,2,3$しかあり得ないということになる。$\lambda=2,3$の場合を上で考えたが、$\lambda=0$のときは基底を$1$個も取らずに${}_3 \mathrm{C}_0=1$項を構成するので単なる実数と同じになる。$\lambda=1$のときは基底を$1$個だけ取る組合せで${}_3 \mathrm{C}_1=3$項作るので、$p^1 \boldsymbol{e}_1 + p^2 \boldsymbol{e}_2 + p^3 \boldsymbol{e}_3$のような形、つまり通常のベクトルと同じになる。

改めて、一般の場合$\wedge^\lambda \mathbb{R}^n$つまり$n$次元ベクトル$\mathbb{R}^n$の$\lambda$重積について考えてみる。

$\boldsymbol{p}_1,\cdots,\boldsymbol{p}_\lambda \in \mathbb{R}^n$に対して

$\boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_\lambda = \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn} (\sigma) \boldsymbol{p}_{\sigma(1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma(\lambda)}$
であった。

$\boldsymbol{p}_{[1]} = ({p_{[1]}}^1,{p_{[1]}}^2,\cdots,{p_{[1]}}^n)$

$\boldsymbol{p}_{[2]} = ({p_{[2]}}^1,{p_{[2]}}^2,\cdots,{p_{[2]}}^n)$

$\vdots$

$\boldsymbol{p}_{[\lambda]} = ({p_{[\lambda]}}^1,{p_{[\lambda]}}^2,\cdots,{p_{[\lambda]}}^n)$

と成分表示すると、

$\boldsymbol{p}_{[1]} \wedge \boldsymbol{p}_{[2]} \wedge \cdots \wedge \boldsymbol{p}_{[\lambda]}$

$= \displaystyle \sum_{i_1 ～ i_\lambda}^{{}_n \mathrm{C}_\lambda {\rm 通り}} \left( \displaystyle \sum_{\sigma}^{\lambda ! {\rm 通り}} \mathrm{sgn} (\sigma)~{p_{[1]}}^\sigma(i_1) {p_{[2]}}^\sigma(i_2) \cdots {p_{[\lambda]}}^\sigma(i_\lambda) \right) \boldsymbol{e}_{i_1} \wedge \boldsymbol{e}_{i_2} \wedge \cdots \wedge \boldsymbol{e}_{i_\lambda}$

となる。

これを示す。

$\lambda$重ウェッジ積はテンソル積を用いて

$\boldsymbol{p}_{[1]} \wedge \cdots \wedge \boldsymbol{p}_{[\lambda]} = \displaystyle \sum_{i_1 ～ i_\lambda}^{{}_n \mathrm{C}_\lambda 通り} \mathrm{sgn} (\sigma)~\boldsymbol{p}_{[\sigma(1)]} \otimes \cdots \otimes \boldsymbol{p}_{[\sigma(\lambda)]}$

と定義される。

$\boldsymbol{p}_{[\sigma(1)]} \otimes \cdots \otimes \boldsymbol{p}_{[\sigma(\lambda)]}$

というテンソル積は、

$\displaystyle \sum_{i_1 = 1}^{n} \cdots \displaystyle \sum_{i_\lambda = 1}^{n} {p_{[\sigma(1)]}}^{i_1} \cdots {p_{[\sigma(\lambda)]}}^{i_\lambda} \boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_{i_\lambda}$

である。$i_1,\cdots,i_\lambda$のそれぞれが独立に$1$～$n$を動き、その全てのパターンの和を取るので$n^\lambda$項の和である。

この中には、

①$\lambda$個連なった$\boldsymbol{e}$の添字に2つ以上の重複がある項（例えば$\lambda=3$なら$\boldsymbol{e}_2 \otimes \boldsymbol{e}_1 \otimes \boldsymbol{e}_2$など）

もあるし、

②重複が全くない項（$\lambda=3$なら$\boldsymbol{e}_1 \otimes \boldsymbol{e}_3 \otimes \boldsymbol{e}_2$など）

もある。

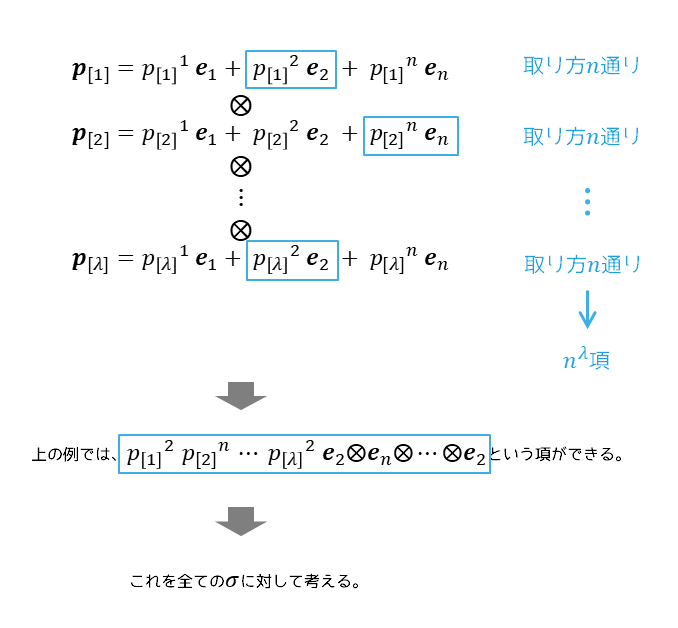
ただし、全ての置換$\sigma$について和を取ると、前述の①は符号の正負関係により上手く相殺されて$0$になってしまい、②だけが生き残るのである。

もう少し詳しく説明しよう。

①の場合に$\sigma$について和を取るとはどういうことか。

①の場合とは、$\lambda$個連なった$\boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_{i_\lambda}$の中に2つ以上の重複があるときであり、このとき係数の${p_{[\sigma(1)]}}^{i_1} \cdots {p_{[\sigma(\lambda)]}}^{i_\lambda}$の右上の添字も同じ重複の仕方をしている。

$\sigma$について和を取るとき、この右上の添字の並びを固定して右下の$\sigma(1),\cdots,\sigma(\lambda)$を様々にシャッフルして足していくことになる。

このときどういうことが起こるか。

右上の添字に同じ値$I$が$\lambda’ (2 \leqq\leqq \lambda)$個含まれるとしよう。そのような項の1つは

${p_{[\sigma (1)]}}^{i_1} \cdots {p_{[\sigma (k_1)]}}^{I} \cdots {p_{[\sigma (k_2)]}}^{I} \cdots \cdots {p_{[\sigma (k_{\lambda’})]}}^{I} \cdots {p_{[\sigma (\lambda)]}}^{i_\lambda} \boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_I \cdots \boldsymbol{e}_I \cdots \cdots \boldsymbol{e}_I \cdots \boldsymbol{e}_{i_\lambda}$
であり、これに対する右下のシャッフルの仕方は「$\lambda$個中に同じものを$\lambda’$個含む同含順列」である。

つまり並べ方は$\cfrac{\lambda !}{\lambda’ !}$通りある。

だがこれは同じもの$\lambda’$個を区別しない数え方であることに注意が必要だ。上のテンソル積は$n^\lambda~\lambda !$個を全て網羅して足し上げる計算なので見かけが同じでも勝手に区別を外すべきではない。

なので改めて区別を付けることにすると、$\cfrac{\lambda !}{\lambda’ !}$通りの各々に対し、$\lambda’$個の$I$の並べ方$\lambda’ !$通りが存在するということになる。

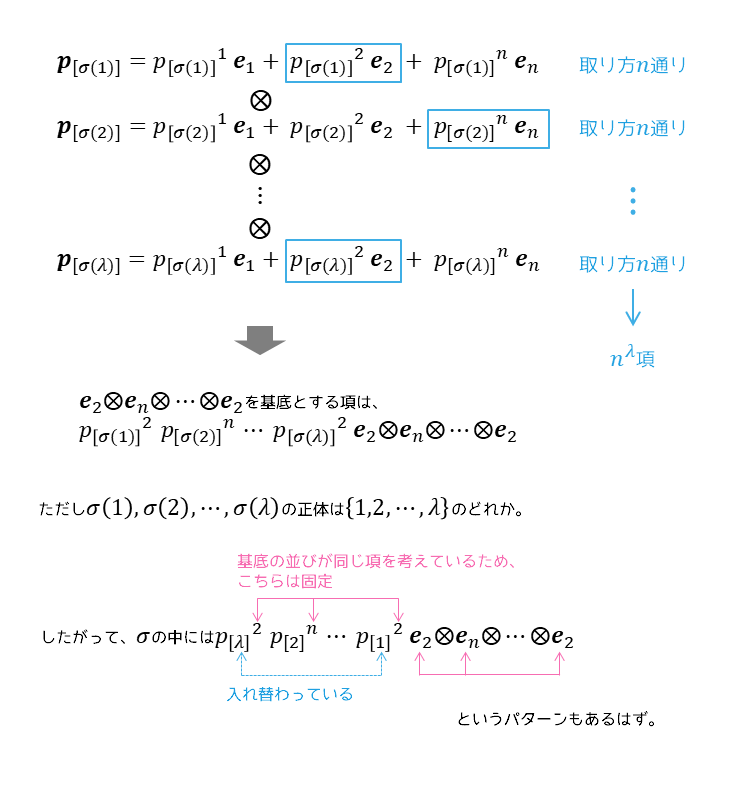
さらに上式の係数部分はただの実数の積なので掛ける順番を入れ替えても絶対値としては同じである。

つまり$\lambda’ !$通りには

${p_{[\sigma (1)]}}^{i_1} \cdots {p_{[\sigma (k_2)]}}^{I} \cdots {p_{[\sigma (k_1)]}}^{I} \cdots \cdots {p_{[\sigma (k_{\lambda’})]}}^{I} \cdots {p_{[\sigma (\lambda)]}}^{i_\lambda} \boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_I \cdots \boldsymbol{e}_I \cdots \cdots \boldsymbol{e}_I \cdots \boldsymbol{e}_{i_\lambda}$

や

${p_{[\sigma (1)]}}^{i_1} \cdots {p_{[\sigma (k_\lambda’)]}}^{I} \cdots {p_{[\sigma (k_1)]}}^{I} \cdots \cdots {p_{[\sigma (k_{2})]}}^{I} \cdots {p_{[\sigma (\lambda)]}}^{i_\lambda} \boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_I \cdots \boldsymbol{e}_I \cdots \cdots \boldsymbol{e}_I \cdots \boldsymbol{e}_{i_\lambda}$

などが含まれる。右上が$I$のものどうしでシャッフルされ、それ以外の項は固定されていることに注意されたい。

しかし結局は同じものをシャッフルしているだけなので、ただの実数の積である係数は全く同じ数値のままである。

こんなことが起こるのは右上が同じものどうしのシャッフルの場合に限られる。試しに右上が異なるものものどうしを入れ替えてみると、

${p_{[\sigma (\lambda)]}}^{i_1} \cdots {p_{[\sigma (k_1)]}}^{I} \cdots {p_{[\sigma (k_2)]}}^{I} \cdots \cdots {p_{[\sigma (k_{\lambda’})]}}^{I} \cdots {p_{[\sigma (1)]}}^{i_\lambda} \boldsymbol{e}_{i_1} \otimes \cdots \otimes \boldsymbol{e}_I \cdots \boldsymbol{e}_I \cdots \cdots \boldsymbol{e}_I \cdots \boldsymbol{e}_{i_\lambda}$

などができるが、これは元の項と同じものではない。$\lambda’$通りには含まれないパターンである。

そして、これらを足し上げるに当たって$\mathrm{sgn} (\sigma)$を付けなければならないわけだが、$2$以上の$\lambda’$に対して$\lambda’ !$通りの置換のうち半分が偶置換、半分が奇置換であるを前ページで証明済みである。

したがってこれらの$\lambda’ !$項を全部足すと、絶対値は全て同じで半分が＋、半分が－なのでトータルで$0$になるということである。

このことを踏まえると、$n$次元空間のベクトルの$\lambda$重ウェッジ積は以下のように書き換えることができる。

$\boldsymbol{p}_{[1]} \wedge \cdots \wedge \boldsymbol{p}_{[\lambda]} = \displaystyle \sum_{i_1～i_\lambda}^{{}_n \mathrm{C}_\lambda {\rm 通り}} \left( \displaystyle \sum_{\sigma}^{\lambda ! {\rm 通り}} \mathrm{sgn} (\sigma)~{p_{[1]}}^{\sigma (i_1)} \cdots p_{[\lambda]}^{\sigma (i_\lambda)} \right) \boldsymbol{e}_{i_1} \wedge \cdots \wedge \boldsymbol{e}_{i_\lambda} \in \wedge^\lambda V^n$

$\lambda$重テンソル積は$\lambda$階テンソルである。$\boldsymbol{p}_1 \otimes \cdots \otimes \boldsymbol{p}_\lambda$の$(i_1,\cdots,i_\lambda)$成分を$(\boldsymbol{p}_1 \otimes \cdots \otimes \boldsymbol{p}_\lambda)^{i_1,\cdots,i_\lambda}$のように書くとその変換則は

$(\boldsymbol{p’}_1 \otimes \cdots \otimes \boldsymbol{p’}_\lambda)^{i_1,\cdots,i_\lambda} = {a^{i_1}}_{j_1} \cdots {a^{i_\lambda}}_{j_\lambda} (\boldsymbol{p}_1 \otimes \cdots \otimes \boldsymbol{p}_\lambda)^{j_1,\cdots,j_\lambda}$

であり、括弧の中身の$\lambda$重テンソル積の順序を並べ替えることを考えると、これは$\lambda !$種類ある。半分は偶置換、半分は奇置換である。偶置換であるものを足し、奇置換であるものを引くと

$\left( \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn}(\sigma)~\boldsymbol{p’}_{\sigma(1)} \otimes \cdots \otimes \boldsymbol{p’}_{\sigma (\lambda)} \right)^{i_1,\cdots,i_\lambda} = {a^{i_1}}_{j_1} \cdots {a^{i_\lambda}}_{j_\lambda} \left( \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn}(\sigma)~\boldsymbol{p}_{\sigma(1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)} \right)^{j_1,\cdots,j_\lambda}$

つまり

$(\boldsymbol{p’}_1 \wedge \cdots \wedge \boldsymbol{p’}_\lambda)^{i_1,\cdots,i_\lambda} = {a^{i_1}}_{j_1} \cdots {a^{i_\lambda}}_{j_\lambda} (\boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_\lambda)^{j_1,\cdots,j_\lambda}$

となり、$\lambda$重ウェッジ積は$\lambda$階テンソルの変換則に従う。

$\lambda$重ウェッジ積は$\lambda$階テンソルなので、当然ながら$\lambda$重線型性を持つ。一応確認しておこう。

$\boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_{\mu-1} \wedge \boldsymbol{p}_\mu \wedge \boldsymbol{p}_{\mu+1} \wedge \cdots \wedge \boldsymbol{p}_\lambda$

において、$\boldsymbol{p}_\mu = \alpha \boldsymbol{q} + \beta \boldsymbol{r}$であるとすると

$= \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn}(\sigma)~(\boldsymbol{p}_{\sigma (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)})$（積の中のどれかに$\boldsymbol{p}_\mu$が含まれている）

$= \displaystyle \sum_{\sigma \in S_\lambda} (\alpha \boldsymbol{p}_{\sigma (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)} + \beta \boldsymbol{p}_{\sigma (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)})$（括弧内第１項には$\boldsymbol{q}$が、第２項には$\boldsymbol{r}$が含まれている）

$= \alpha \displaystyle \sum_{\sigma \in S_\lambda} \boldsymbol{p}_{\sigma (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)} + \beta \displaystyle \sum_{\sigma \in S_\lambda} \boldsymbol{p}_{\sigma (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\lambda)}$（　〃　）

$= \alpha \boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_{\mu-1} \wedge \boldsymbol{q} \wedge \boldsymbol{p}_{\mu+1} \wedge \cdots \wedge \boldsymbol{p}_\lambda + \beta \boldsymbol{p}_1 \wedge \cdots \wedge \boldsymbol{p}_{\mu-1} \wedge \boldsymbol{q} \wedge \boldsymbol{p}_{\mu+1} \wedge \cdots \wedge \boldsymbol{p}_\lambda$（　〃　）

よって、$\lambda$重ウェッジ積は$\lambda$重線型性を持つ。

$\lambda$重線型性を考慮すれば、$\wedge^\lambda \mathbb{R}^n$の元である$\lambda$重ウェッジ積は「$n$個から$\lambda$個取る組合せ」${}_n \mathrm{C}_\lambda$項の和になる。

偶置換を$\sigma^{\prime \prime}$、奇置換を$\sigma^\prime$と表す。また、連続して2回の置換を行うとこれは合成された1回の置換を行うのと同じことなので、$\sigma_1 \to \sigma_2$の”合成置換”を合成関数の記法に倣って$\sigma_2 \circ \sigma_1$のように表記することにする。

$\{ 1,\cdots,\lambda \}$に偶置換を適用した並び$\{ \sigma^{\prime \prime}(1),\cdots,\sigma^{\prime \prime}(\lambda) \}$を考え、この順に掛けたウェッジ積は

$\boldsymbol{p}_{\sigma^{\prime \prime} (1)} \wedge \cdots \wedge \boldsymbol{p}_{\sigma^{\prime \prime} (\lambda)}$

$= \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn} (\sigma)~\boldsymbol{p}_{\sigma (\sigma^{\prime \prime} (1))} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\sigma^{\prime \prime} (\lambda))}$

$= \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn} (\sigma)~\boldsymbol{p}_{\sigma \circ \sigma^{\prime \prime} (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma \circ \sigma^{\prime \prime} (\lambda)}$

ここで考察が必要なのだが、一度偶置換$\sigma^{\prime \prime}$を適用されてできた並び$\{ \sigma(1),\cdots,\sigma(\lambda) \}$に対してさらに置換を考えその全パターンの総和を取るということをしているが、これはそもそもの並び$\{ 1,\cdots,\lambda \}$に対する1回の置換の全パターンの総和を取るというのと結局は同じである。ただし注意が必要なのは$\mathrm{sgn} (\sigma)$であり、これは2回目の置換の偶奇を表している。1回目が偶置換なので

$\begin{cases}
\sigma {\rm ：偶置換　のとき、} \sigma \circ \sigma^{\prime \prime} {\rm ：偶置換（偶+偶だから）}\\
\sigma {\rm ：奇置換　のとき、} \sigma \circ \sigma^{\prime \prime} {\rm ：奇置換（偶+奇だから）}
\end{cases}$

より、$\mathrm{sgn} (\sigma) = \mathrm{sgn} (\sigma \circ \sigma^{\prime \prime})$となり、
$= \displaystyle \sum_{\sigma \circ \sigma^{\prime \prime} \in S_\lambda} \mathrm{sgn} (\sigma \circ \sigma^{\prime \prime})~\boldsymbol{p}_{\sigma \circ \sigma^{\prime \prime} (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma \circ \sigma^{\prime \prime} (\lambda)}$

同様に$\{ 1,\cdots,\lambda \}$に奇置換を適用した並び$\{ \sigma^\prime(1),\cdots,\sigma^\prime(\lambda) \}$を考え、この順に掛けたウェッジ積は

$\boldsymbol{p}_{\sigma^\prime (1)} \wedge \cdots \wedge \boldsymbol{p}_{\sigma^\prime (\lambda)}$

$= \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn} (\sigma)~\boldsymbol{p}_{\sigma (\sigma^\prime (1))} \otimes \cdots \otimes \boldsymbol{p}_{\sigma (\sigma^\prime (\lambda))}$

$= \displaystyle \sum_{\sigma \in S_\lambda} \mathrm{sgn} (\sigma)~\boldsymbol{p}_{\sigma \circ \sigma^\prime (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma \circ \sigma^\prime (\lambda)}$

この場合の$\mathrm{sgn} (\sigma)$について考えると、

$\begin{cases}
\sigma {\rm ：偶置換　のとき、} \sigma \circ \sigma^\prime {\rm ：奇置換（奇+偶だから）}\\
\sigma {\rm ：奇置換　のとき、} \sigma \circ \sigma^\prime {\rm ：偶置換（奇+奇だから）}
\end{cases}$

より、$\mathrm{sgn} (\sigma) = -\mathrm{sgn} (\sigma \circ \sigma^\prime)$となり、

$= \displaystyle \sum_{\sigma \circ \sigma^\prime \in S_\lambda} -\mathrm{sgn} (\sigma \circ \sigma^\prime)~\boldsymbol{p}_{\sigma \circ \sigma^\prime (1)} \otimes \cdots \otimes \boldsymbol{p}_{\sigma \circ \sigma^\prime (\lambda)}$

したがって、

$\boldsymbol{p}_{\sigma^{\prime \prime} (1)} \wedge \cdots \wedge \boldsymbol{p}_{\sigma^{\prime \prime} (\lambda)} = – \boldsymbol{p}_{\sigma^\prime (1)} \wedge \cdots \wedge \boldsymbol{p}_{\sigma^\prime (\lambda)}$
つまり偶置換の順のウェッジ積と奇置換の順のウェッジ積は符号が逆になり、$\lambda$重ウェッジ積が交代性（反対称性）を持つことが示された。