4.直交行列：回転変換

2次元における回転変換は、高校数学でも（学習指導要領に含まれていた世代の人は）おなじみの次の行列で表される1次変換である。

$R =
\begin{pmatrix}
\cos \theta & -\sin \theta\\
\sin \theta & \cos \theta
\end{pmatrix}$

3次元における回転変換であるロドリゲスの回転公式を導出する。

図で$\overrightarrow{\mathrm{OP}}$を$\theta$

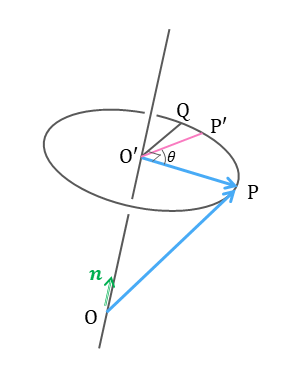
動かしたものを$\overrightarrow{\mathrm{OP’}}$、$\cfrac{\pi}{2}$動かしたものを$\overrightarrow{\mathrm{OQ}}$とすると

$\overrightarrow{\mathrm{OP’}} = \overrightarrow{\mathrm{OO’}} + \overrightarrow{\mathrm{O’P’}}$
$\overrightarrow{\mathrm{OO’}} = (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n}$

また

$\overrightarrow{\mathrm{O’P’}} = \overrightarrow{\mathrm{O’P}} \cos \theta + \overrightarrow{\mathrm{O’Q}} \sin \theta$

$\overrightarrow{\mathrm{O’P}} = \overrightarrow{\mathrm{OP}} – \overrightarrow{\mathrm{OO’}} = \overrightarrow{\mathrm{OP}} – (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n}$

$\overrightarrow{\mathrm{O’Q}} = \boldsymbol{n} \times \overrightarrow{\mathrm{O’P}} = \boldsymbol{n} \times \{ \overrightarrow{\mathrm{OP}} – (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n} \} = \boldsymbol{n} \times \overrightarrow{\mathrm{OP}}$

なので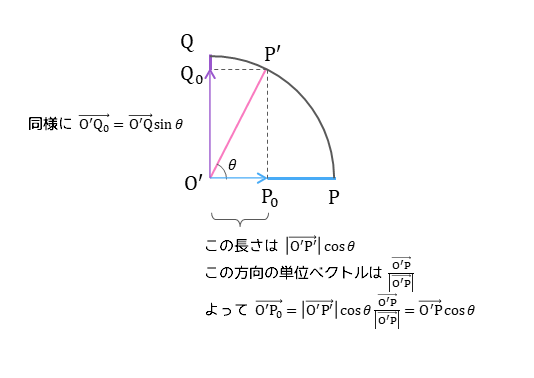$\overrightarrow{\mathrm{OP’}} = (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n} + \cos \theta \{ \overrightarrow{\mathrm{OP}} – (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n} \} + \sin \theta (\boldsymbol{n} \times \overrightarrow{\mathrm{OP}})$

$= \cos \theta \overrightarrow{\mathrm{OP}} + (1 – \cos \theta) (\overrightarrow{\mathrm{OP}} \cdot \boldsymbol{n}) \boldsymbol{n} + \sin \theta (\boldsymbol{n} \times \overrightarrow{\mathrm{OP}})$

ここで$(\boldsymbol{x} \cdot \boldsymbol{a}) \boldsymbol{a}$は次のように書き換えることができる。

$(\boldsymbol{x} \cdot \boldsymbol{a}) \boldsymbol{a}
= \left\{ \begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix}
\begin{pmatrix}
a_1\\
a_2\\
a_3
\end{pmatrix} \right\}
\begin{pmatrix}
a_1\\
a_2\\
a_3
\end{pmatrix}
= (a_1 x_1 + a_2 x_2 + a_3 x_3)
\begin{pmatrix}
a_1\\
a_2\\
a_3
\end{pmatrix}
= \begin{pmatrix}
{a_1}^2 x_1 + a_1 a_2 x_2 + a_1 a_3 x_3\\
a_2 a_1 x_1 + {a_2}^2 x_2 + a_2 a_3 x_3\\
a_3 a_1 x_1 + a_3 a_2 x_2 + {a_3}^2 x_3
\end{pmatrix}$
$= \begin{pmatrix}
{a_1}^2 & a_1 a_2 & a_1 a_3\\
a_2 a_1 & {a_2}^2 & a_2 a_3\\
a_3 a_1 & a_3 a_2 & {a_3}^2
\end{pmatrix}
\begin{pmatrix}
x_1\\
x_2\\
x_3
\end{pmatrix}
= \left\{ \begin{pmatrix}
a_1\\
a_2\\
a_3
\end{pmatrix}
\begin{pmatrix}
a_1 & a_2 & a_3
\end{pmatrix} \right\}
\begin{pmatrix}
x_1\\
x_2\\
x_3
\end{pmatrix}
= \boldsymbol{a}~{}^T \boldsymbol{a}~\boldsymbol{x}$

また$\boldsymbol{a} \times \boldsymbol{x} = – \hat{A} \boldsymbol{x}$なので、

$\overrightarrow{\mathrm{OP’}} = \cos \theta \overrightarrow{\mathrm{OP}} + (1 – \cos \theta) \boldsymbol{n}~{}^T \boldsymbol{n} \overrightarrow{\mathrm{OP}} – \sin \theta \hat{N} \overrightarrow{\mathrm{OP}}$

$= \{ \cos \theta E + (1 – \cos \theta) \boldsymbol{n}~{}^T \boldsymbol{n} – \sin \theta \hat{N} \} \overrightarrow{\mathrm{OP}}$

ロドリゲスの回転公式を構成する列ベクトルが正規直交基底をなすことを確認する。

$\{ \cos \theta + {n_x}^2 (1 – \cos \theta) \}^2 + \{ n_y n_x (1 – \cos \theta) + n_z \sin \theta \}^2 + \{ n_z n_x (1 – \cos \theta) – n_y \sin \theta \}^2$

$= \cos^2 \theta + 2 {n_x}^2 \cos \theta (1 – \cos \theta) + {n_x}^4 (1 – \cos \theta)^2$

$+ {n_x}^2 {n_y}^2 (1 – \cos \theta)^2 + 2 n_y n_x n_z \sin \theta (1 – \cos \theta) + {n_z}^2 \sin^2 \theta$

$+ {n_z}^2 {n_x}^2 (1 – \cos \theta)^2 – 2 n_x n_y n_z \sin \theta (1 – \cos \theta) + {n_y}^2 \sin^2 \theta$

$= \cos^2 \theta + 2 {n_x}^2 \cos \theta (1 – \cos \theta) + {n_x}^4 (1 – \cos \theta)^2$

$+ {n_x}^2 {n_y}^2 (1 – \cos \theta)^2 + {n_z}^2 \sin^2 \theta$

$+ {n_z}^2 {n_x}^2 (1 – \cos \theta)^2 + {n_y}^2 \sin^2 \theta$

これをどう整理するかは人それぞれだと思うが、ロドリゲスの回転公式における$\boldsymbol{n}$は回転軸方向の単位ベクトルなので${n_x}^2 + {n_y}^2 + {n_z}^2 = 1$であることを利用すれば、

$= 1$

となる。

$\{ \cos \theta + {n_x}^2 (1 – \cos \theta) \} \{ n_x n_y (1 – \cos \theta) – n_z \sin \theta \} + \{n_y n_x (1 – \cos \theta) + n_z \sin \theta \} \{ \cos \theta + {n_y}^2 (1 – \cos \theta) \} + \{n_z n_x (1 – \cos \theta) – n_y \sin \theta \} \{ n_z n_y (1 – \cos \theta) + n_x \sin \theta \}$

$= n_x n_y \cos \theta (1 – \cos \theta) – n_z \sin \theta \cos \theta + {n_x}^3 n_y (1 – \cos \theta)^2 – {n_x}^2 n_z (1 – \cos \theta) \sin \theta$

$+ n_x n_y \cos \theta (1 – \cos \theta) + n_x {n_y}^3 (1 – \cos \theta)^2 + n_z \sin \theta \cos \theta + {n_y}^2 n_z (1 – \cos \theta) \sin \theta$

$+ n_x n_y {n_z}^2 (1 – \cos \theta)^2 + {n_x}^2 n_z (1 – \cos \theta) \sin \theta – {n_y}^2 n_z (1 – \cos \theta) \sin \theta – n_x n_y \sin^2 \theta$

$= n_x n_y (1 – \cos \theta)^2 + 2 n_x n_y \cos \theta (1 – \cos \theta) – n_x n_y (1 – \cos^2 \theta)$

$= 0$

また、右手系であることを確認する。

第$1$列から順に$\boldsymbol{r}_1,~\boldsymbol{r}_2,~\boldsymbol{r}_3$として$\boldsymbol{r}_1 \times \boldsymbol{r}_2$を計算してみる。

第1成分

$\{ n_y n_x (1 – \cos \theta) + n_z \sin \theta \} \{ n_z n_y (1 – \cos \theta) + n_x \sin \theta \} – \{ \cos \theta + {n_y}^2 (1 – \cos \theta) \} \{ n_z n_x (1 – \cos \theta) – n_y \sin \theta \}$

$= n_x {n_y}^2 n_z (1 – \cos \theta)^2 + {n_x}^2 n_y (1 – \cos \theta) \sin \theta + n_y {n_z}^2 (1 – \cos \theta) \sin \theta + n_x n_z \sin^2 \theta$

$- n_x n_z \cos \theta (1 – \cos \theta) + n_y \sin \theta \cos \theta – n_x {n_y}^2 n_z (1 – \cos \theta)^2 + {n_y}^3 (1 – \cos \theta) \sin \theta$

$= n_x n_z (1 – \cos \theta) + n_y \sin \theta$

第2成分

$\{ n_z n_x (1 – \cos \theta) – n_y \sin \theta \} \{ n_x n_y (1 – \cos \theta) – n_z \sin \theta \} – \{ n_z n_y (1 – \cos \theta) + n_x \sin \theta \} \{ \cos \theta + {n_x}^2 (1 – \cos \theta) \}$

$= {n_x}^2 n_y n_z (1 – \cos \theta)^2 – n_x {n_z}^2 (1 – \cos \theta) \sin \theta – n_x {n_y}^2 (1 – \cos \theta) \sin \theta + n_y n_z \sin^2 \theta$

$- n_y n_z \cos \theta (1 – \cos \theta) – {n_x}^2 n_y n_z (1 – \cos \theta)^2 – n_x \sin \theta \cos \theta – {n_x}^3 (1 – \cos \theta) \sin \theta$

$= n_y n_z (1 – \cos \theta) – n_x \sin \theta$

第3成分

$\{ \cos \theta + {n_x}^2 (1 – \cos \theta) \} \{ \cos \theta + {n_y}^2 (1 – \cos \theta) \} – \{ n_x n_y (1 – \cos \theta) – n_z \sin \theta \} \{ n_y n_x (1 – \cos \theta) + n_z \sin \theta \}$

$= \cos^2 \theta + {n_y}^2 \cos \theta (1 – \cos \theta) + {n_x}^2 \cos \theta (1 – \cos \theta) + {n_x}^2 {n_y}^2 (1 – \cos \theta)^2$

$- {n_x}^2 {n_y}^2 (1 – \cos \theta)^2 – n_x n_y n_z (1 – \cos \theta) \sin \theta + n_x n_y n_z (1 – \cos \theta) \sin \theta + {n_z}^2 \sin^2 \theta$

$= \cos \theta + {n_z}^2 (1 – \cos \theta)$

となり、$\boldsymbol{r}_1 \times \boldsymbol{r}_2 = \boldsymbol{r}_3$が成り立っている、つまり右手系である。